まえがき
移調に関して、楽典の教科書には書かれていないことがたくさんあって、自分なりに苦労しながら発見した事実がたくさんある。これから勉強する人のためにそれらの事項を書きとどめておきたい。
12平均律を採用する
ここでは特に断りのない限り、12平均律に限定して話を進める。12平均律では、12ある、それぞれの長調は対等である。C major scale(ハ長調)を半音上に平行移動させるとC# major scaleになる。どの調が偉い(優位である)というわけではない。
属調と下属調への移調について
12ある長調がすべて対等であるということは、C major scaleについて考えたことは、他のどの長調であっても同じ法則が当てはまる。
例えば、C major scaleの属調(G major scale)にいくときにf音(C major scaleの4番目の音)に#がつき、それは属調における7番目の音であるが、この法則は次のように一般化される。
- X major scaleの属調にいくとき4番目の音に#がつき、それは属調における7番目の音である。 ※ Xは12の任意の長調
以下では、この4番目の音を小文字のローマ数字表記でivのように記す。7番目の音であればviiである。
同じく、C major scaleから下属調(F major scale)に移行すると、b音(7番目の音)に♭がつき、それは下属調の4番目の音である。
これも同じく次のように一般化される。
- X major scaleの下属調にいくとき7番目の音に♭がつき、それは下属調における4番目の音である。
属調と下属調の対称性について
属調は主音(≒scaleの開始音)が完全五度上、下属調は主音が完全五度下(=完全四度上)に変わる。つまり、属調と下属調には対称性がある。
さきほどの一般化された法則を再度引用しよう。
- X major scaleの属調にいくとき4番目の音に#がつき、それは属調における7番目の音である。
- X major scaleの下属調にいくとき7番目の音に♭がつき、それは下属調における4番目の音である。
上の2つの法則を見比べてみよう。#と♭、4と7という数字がそれぞれ対称的に現れている。何故なら、「属調の下属調」は、元の調だし、「下属調の属調」も元の調なので、下属調にする操作は属調にする操作の逆変換(≒元に戻す操作)となっていなければならないし、属調にする操作は下属調にする操作の逆変換にもなっていなければならないからである。
ゆえに、属調化する操作と下属調化する操作には対称性がある。
#と♭の対称性
属調化する操作が下属調化する操作の逆変換であることは上で述べたが、ここで、#と♭との対称性についても明らかになった。
- #をつける操作の反対の操作は#を減らす(♭をつける)。
- ♭をつける操作の反対の操作は♭を減らす(#をつける)。
である。
長調と短調
natural minor scale(自然的短音階)は、major scaleの6番目の音から始めた音階であり、C major scaleとA natural minor scaleとは同じ調号である。
12のすべての調は対等なので、X major scaleとXの短3度低いnatural minor scaleとは同じ調号であると一般化できる。
ゆえに、12それぞれのnatural minor scaleは、短3度上のmajor scaleと同じ調号であり、移調を考える上では長調のときの調号で考えれば十分である。そこで、ここではnatural minor scaleの移調については特に触れないが、これは長調の移調と同様の議論が成り立つことは明らかである。
また、自然的短音階以外の短調として、和声的短音階と旋律的短音階(上行)があるが、この2つは長調の調号では表現できないが(例 : A harmonic minor scale = A natural minor scaleのvii音を半音上げたもの)、A harmonic minor scaleを半音上に移動させるとA# harmonic minor scaleになるというように、平行移動させたものには違いないし、また属調化/化属調化の操作はさきほどの議論と同様なので、さきほどまでの議論が通用することがわかる。
そこで以下では「長調」とは書かずに、「短調」を含めて、単に「調」と書く。さきほどまでに導き出した法則は、すべて短調でも成り立つからである。
五度圏(circle of fifths)
属調と下属調には対称性があることがわかったので、以下では属調のほうについてだけ考える。
ある調から、その属調、そのさらに属調というように属調を巡っていくことを考える。
C major scale→G major scale→D major scale→…
いまmajor scaleとnatural minor scaleとは同様の議論が成り立つことがわかっているので、major scaleにこだわる必要はない。そこで主音だけに着目して、c(ド) → g(ソ) → d(レ) → … のような循環を考える。
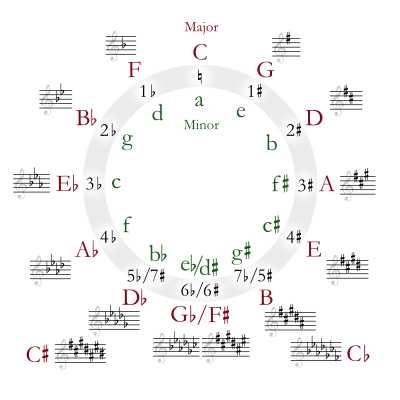
このような循環を五度圏(Circle of fifths)と呼ぶ。
上図を時計回りに回るのが属調(主音が完全5度上)方向への回転であり、反時計回りに回るのが下属調(主音が完全5度下)方向への回転である。
興味深いことに12のすべての調が1回ずつ出現して、最後に元の調に戻ってくる。これはどういうことなのか。
5度圏で12すべての調が出現する理由
5度圏で12すべての調が出現するのは何故なのか。ある音から開始して、完全五度上を辿っていくとすべての音を経由して元の音に戻る。これは何故なのか。従来の音楽理論の教科書にはこの理由は書かれていない。
しかし、整数論を少し知っていれば、この理由は明らかである。つまり、次のように考える。
完全五度上は、半音で表現すると半音7個上である。そのさらに完全五度上は半音14個上(≒半音2個上)である。そのさらに完全五度上は半音21個上(≒半音9個上)である。一般化するとk回の完全五度上を辿ると半音7×k個上である。ただし、12で割った余りが同じだと同じ音なので14なら2というように考えるものとする。これは整数論で出てくるmod(剰余)演算である。
つまり、7k mod 12 (k = 0 , 1 , … 11)が、それぞれ違う数であることを示せば完全五度上を辿っていくときに12音すべてが出現することが証明される。
これは、背理法で簡単に証明できる。
【証明】 0 <= a < b <= 11なる整数a,bを選んだときに、7a mod 12と7b mod 12が一致すると仮定してみよう。7aと7bは12で割った余りが等しいということを意味しているので、このとき7a = 7b + 12n(nは適当な整数)と書ける。7(a-b) = 12n。左辺の(a-b)の項だが、0 <= a < b <= 11なので、この項は1から11までの値しか取れない。どの値を取っても右辺の12が出てこないので、この等式は正しくない。ゆえに、背理法により、題意は証明された。
もう少し一般化すると、半音7個分という7と、12平均律の12の、7と12という数が互いに素であれば、この証明は成り立つ。
つまり、53平均律のようなものを考えたときも、完全X度が半音n個分だとして、53とnが互いに素であるような数であれば、完全X度上を繰り返すと53のすべての音が出現することになる。
調号から主音の見つけ方
五度圏の図を見ると、五度圏を時計回り(完全五度上方向のまわり)に回ると調号に#が一つずつ増えていくことがわかる。#が5個〜7個になったあたりから調号は♭に変わり、そのあとも時計まわりに回ると♭が減っていく。
ここにはいくつかの法則がある。親切な楽典の教科書には、次のように書かれているかも知れない。
- 調号に#がつくときは、調号の右端の#の半音上が(長調の時の)主音
- 例) G major scaleだとf音に#がついているのでf#の半音上であるgが(長調の時の)主音。
- 調号に♭がつくときは、調号の右から2番目の♭が(長調の時の)主音
- 例) B♭ major scaleであれば、右から2番目の♭はB♭であるからB♭が(長調の時の)主音。
この覚え方はそこそこ有用であるが、しかし、後者の法則はいま一つである。「右から2番目」と言っても、F major scaleだと♭が1つしかないので、2番目自体がないからである。そもそも五度圏で見て最後についた調号は右端の♭であり、1つ前の♭を基準に考えるのは理にかなっていない。
そこで次のように考えたほうがいいと思う。
- 調号に#がつくときは、調号の右端の#が導音(vii)
- 調号に♭がつくときは、調号の右端の♭が下属音(iv)
- 例) F major scaleであれば、調号の右端の♭はB♭であり、これがivなので完全4度下であるfが(長調のときの)主音。
この法則は、たとえ忘れたとしてもC major scaleからG major scale、F major scaleへ進むときのことを考え、それは12の調が対等であるからどの調でも成り立つことを思い出せば、この法則に自然と辿りつける。
#と♭がつく音についての対称性
調号について、#の付く順序と♭の付く順序もまた対称になっている。
- # ファ・ド・ソ・レ・ラ・ミ・シ
- ♭ シ・ミ・ラ・レ・ソ・ド・ファ
属調・下属調が何故有用なのか
属調と下属調は調号が#か♭一つしか違わないので元の調に近いサウンドセット(音の集合)である。この意味において、和音を借用したりするのに適している。(近いサウンドセットなので元の調とそれほどかけ離れておらず、マッチするはずだという理屈)
半音上への移調
ここまでは属調・下属調ベースで考えてきた。しかし12平均律の最小単位は半音であるから、半音上行、半音下行においてどのように調号が変化するかについても考えておかねばならない。
五度圏の図で時計回りに見て、cから始まって半音上であるd♭が出てくるのは7個目である。時計回り(完全五度上)にいくごとに#が1つつくので、つまり#を7個つければ半音上の調に到達できることがわかる。12の調は対等なので、どの調においてもこの法則は当てはまる。
#と♭の対称性から、#7個をつけることと、♭5個つけることとは同一である。
もう少しいくつか例を出すなら、五度圏の図から、
- #1個つける = ♭11個つける
- #2個つける = ♭10個つける
- #3個つける = ♭9個つける
- #4個つける = ♭8個つける
- #5個つける = ♭7個つける
- #6個つける = ♭6個つける
- #7個つける = ♭5個つける
- #8個つける = ♭4個つける
- #9個つける = ♭3個つける
- #10個つける = ♭2個つける
- #11個つける = ♭1個つける
という法則が成り立つことは明らかである。
これを一般化すると、
- #をn個つける = ♭を12-n個つける ということになる。
- 半音上行で#7個増える=♭5個増える
- 全音(半音2個)上行で、#14個(7×2個)増える=#2個増える(五度圏は12で1周して元の音に戻ってくるので)
- 短三度(半音3個)上行で、#21個(7×3個)増える=#9個増える(12引いた)=♭3個増える(上の法則により)
- 長三度(半音4個)上行で、#28個(7×4個)増える=#4個増える
- 完全四度(半音5個)上行で、#35個(7×5個)増える = #11個増える(12×2引いた) = ♭1個増える
- 完全五度(半音7個)上行で、#49個(7×7個)増える = #1個増える(12×4引いた) のように計算できる。
あるいは、全音上行で#2個増える(という操作)であることはわかるので、長三度(全音二回)上行では、この操作が2回繰り返し適用されて、#4個増えるというのがわかる。
また、すべての調は対等なので、C major scaleについて考えたときのことが一般化できるので、例えば、「C major scaleからD major scaleになると#が2個増える」という事実を知っていれば、「主音が全音上行で#が2個増える」と一般化でき、長3度上行なら、#2個×2回 = #4個増えるのように、主音が全音の整数倍だけ上行するときに#がどう増えるかを導きだすことが出来る。
そして上行と下行は対称性があるので、主音の下行は上行の操作の逆変換となるから、全音上行で#が2個増えるならば、全音下行で#が2個減る(=♭が2個増える)ことがわかる。
結論的にはD♭ major scaleが調号に♭が5個つくことだけ知っていれば、主音の半音上行で♭5個増えると一般化できるので、ここからすべてを導くことが出来る。
D♭ major scaleの♭5個というのが覚えにくければ、D major scaleで#2個というのでも良い。ここから全音上行で#2個増えると一般化でき、これは半音上行を二回繰り返した操作だから、半音上行では、♭5個増える。(#1個増えるのほうは、属調のときなので間違えないように!) 全音上行で♭5個×2 = ♭10個増える = #2個増えるだから、これで合ってる。
鍵盤奏者のための調号一覧
鍵盤上で見て以下のようになる。
- 【♭5】【♭3】 【♭6】【♭4】【♭2】
- 【0】 【#2】 【#4】 【♭1】【 #1】【#3】【#5】
♭6=#6であることはすでに述べた。また、全音上行で#2個増える=♭2個減るなので、それを理解しているとド→レ→ミのところと、ファ→ソ→ラ→シのように全音関係になっているところは自ずと導けるはずである。また半音上行で♭5個増える(#5個減る)なので、ド→レ♭や、ミ→ファ、ファ→ソ♭のところは理解できるはずである。
また全音上行で#2個増える、下属調化で♭1個増えるというのだけでも知っていればファのところが♭1は確定するので、ド→ミは全音2回で#4個増えて、ファが♭1個なので、ミ→ファが#5個減る(♭5個増える)が導けるので、このことからも半音上行で♭5個増えるが導ける。
対称性があるので、半音上行で♭5増えるし、半音下行で#5増える。つまり、C→D♭→D→…という半音上行の循環と、C→B→B♭→…という半音下行の循環とでは調号の付き方に対称性がある。
- C 0
- D♭ ♭5
- D ♯2
- E♭ ♭3
- E ♯4
- F ♭1
- F♯G♭ ♯6・♭6
- G ♯1
- A♭ ♭4
- A ♯3
- B♭ ♭2
- B ♯5
- C 0
まあ、上で書いてきた法則のうちのいくつかだけでも覚えていればこれらは自ずと導けるわけである。
移調奏の方法論
次にピアノなどの演奏において頭のなかで楽譜を移調をしながら演奏するということがどうやれば可能であるのかについて書いていく。
楽譜上、12のmajor scaleおよびその平行調(自然的短音階)においては、調号は変わるものの、臨時記号はつかない。この事実は何を意味するのか。
符頭(音符のオタマジャクシ)が同じ位置(高さ)にあれば、臨時記号はつかないので一つの音が定まるということである。また調が変わっても楽譜の上下の幅が伸びるわけではないので、つまり、1オクターブの7音はそれぞれの位置に収まるということである。
わかりにくいかも知れないので具体的に説明する。C major scaleにおけるド・レ・ミ・ファ・ソ・ラ・シ・ドを楽譜上に書くとする。このとき符頭はそれぞれ違う位置(高さ)にある。このとき符頭の配置されるべき場所は8つ(高いほうのドも含めて)ある。
音程の表現で、ユニゾンを「1度」、1オクターブを「8度」と表現するが、この「X度」というのは、この符頭の配置される場所に着目した表現である。
どの調であっても、1オクターブは7つの音で構成されており(高いほうの主音も含めると8つ)、7つの音を使うことはどの調でも同じなので、符頭の配置場所を増やす必要はない。あくまで調号で辻褄を合わせておけば、なんとかなるはずだ。
具体的に考えてみよう。C major scaleをG major scaleに移調するときについてだ。
- C major scale : ドレミファソラシド
- G major scale : ソラシドレミファ#ソ
楽譜上に書きだしてみればわかるが、平行移動すればぴったり合致する。(ファ#の#は調号についていて、臨時記号としては表現されていないので)
つまり、この移調奏は、ドの音を見たら、ソの音というように、符頭(オタマジャクシ)が五度上の位置にあるものとして捉えればいい。シの音を見たら→五度上=ファ、そして、調号はファに#がつくので、この音はファ#。というように、移調後の調号を考慮して#とか♭をつければ良い。(元の調号の#と♭は気にしなくて良い)
これが移調奏の基本である。
ヘ音記号を見たら、その三度上に符頭があるように脳内変換すればト音記号のときの音と同一になるので、三度上にあるかのようにみなして演奏する訓練をすると思うが、それと同様に、二度、四度、五度、六度、七度上にあるかのようにみなして(移調後の調の調号を考慮しながら)演奏するのが移調奏である。
移調奏の実施例
- 実施例1
いま、E major scaleで楽譜が書かれていたとして、「歌いにくいから半音上げて」と言われたとしよう。
E major scaleは#4個、半音上げたF major scaleは♭1個である。E major scaleの主音はe(ミ)であり、F major scaleの主音はf(ファ)であるから、符頭の位置が一つ(二度)違う。そこで、符頭が二度上にあるものと脳内で変換しながら、その変換後の符頭がシにあるときだけ♭をつければ良い。
- 実施例2
いま、C major scaleで楽譜が書かれていたとして、「歌いにくいから半音上げて」と言われたとしよう。
C major scaleは#も♭もつかない。半音上げたD♭ major scaleは♭5個。符頭の位置が二度違う。そこで符頭が二度上にあるものと脳内変換しながら、変換後の符頭が5つの♭のつく場所(レ、ミ、ソ、ラ、シ)であれば♭をつければ良い。
別解としては、半音上げたのをD♭ major scaleではなく、C# major scaleだとみなす。♭5 = #7であることは先に述べた。C major scaleとC# major scaleであれば主音が同じなので符頭の位置変換は不要であり、単に調号が違うだけである。#が7個つくものとして演奏すれば良い。
ハ長調への移調
ハ長調で考えないと和音進行が分かりづらいという人が多い。12それぞれの調が対等であるとは言っても、それぞれの調でのI,VI,V7に相当する和音が何であるかは即座に言えるためにはそれ相応の訓練を必要とするからである。
そこでハ長調に(頭のなかで)移調してしまうことが考えられる。
ハ長調への移調は実は極めて簡単である。移調奏は移調後の調号に応じて#とか♭をつけなければならないが、ハ長調であれば#も♭もつかないので、つまり、何もつけなくていいのである。
何も考えずに符頭の位置変換だけすれば良い。
例) F major scale → C major scaleへの移調であれば、主音は4度下に移動するので、符頭を4度下にあるものとみなして演奏すれば良い。移調後の調号には#も♭もつかない。つまり、F major scaleのシの音は♭がつくが、4度下のファにするときに♭は不要。
例) C# major scale → C major scaleへの移調であれば、主音は同じ、ドの位置に符頭があるので、符頭の位置変換すら不要。単に調号に#も♭もつかないものとしてそのまま演奏すればいいだけ!
このように符頭の位置変換(時にはそれすら不要)をするだけで、良いので和音を頭のなかで上下に平行移動させて理解できれば、ハ長調であるものとして考えることが出来る。
移調における臨時記号の扱い
和声的短音階では、viiの音を導音として使えるように半音上げる。A harmonic minor scaleであれば、ソの音が半音上がって臨時記号の#がつく。C major scaleとして見たときは5番目の音に#がついているように見える。
- 5番目の音が調号によりすでに#がついている場合、この#はそれよりさらに半音高い音にしないといけないのでダブルシャープで表される。
- 5番目の音が調号によりすでに♭がついている場合、この#はそれよりさらに半音高い音にしないといけないのでナチュラルで表される。
つまり、調号に#がつくときのダブルシャープはmajor scaleから見て半音上げてあるわけだ。調号に♭がつくときのナチュラルも同様である。
そこで、これらの音は移調後も移調した調において半音上げなくてはならない。ここまで読んできた人には造作も無いことだろうから、具体的な説明は省略する。
まとめ
今回は移調後の調号の変化について深く考察をした。移調奏の手助けとなれば幸いである。